Co-Optimization of Design and Fabrication Plans for Carpentry
ACM Transactions on Graphics (Presented on SIGGRAPH 2022)
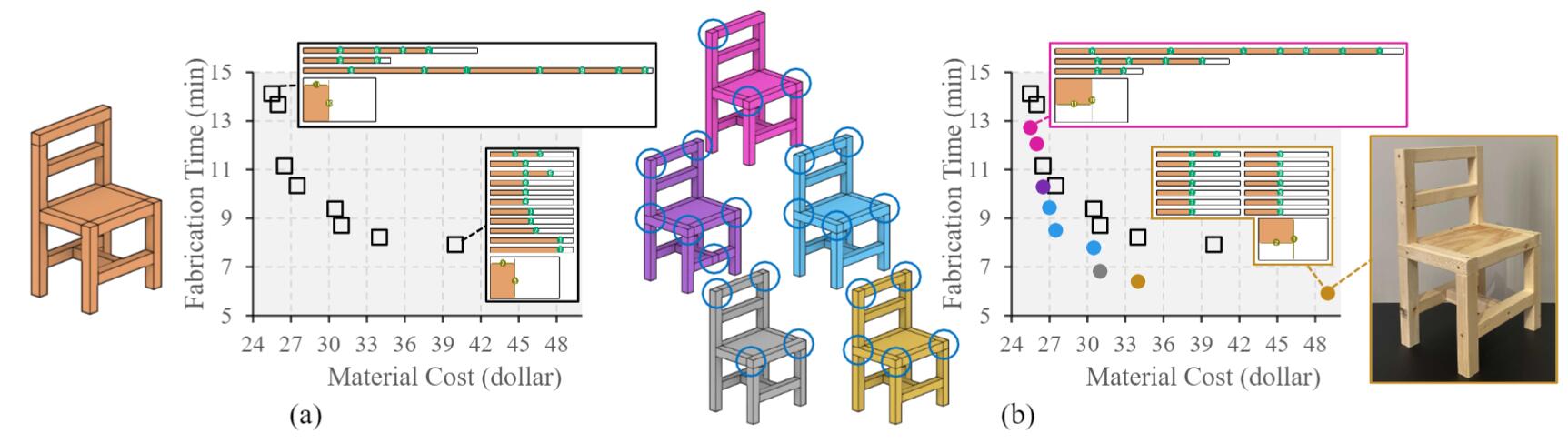
Our system jointly explores the space of discrete design variants and fabrication plans to generate a Pareto front of (design, fabrication plan) pairs that minimize fabrication cost. In this figure, (a) is the input design for a chair and the Pareto front that only explores the space of fabrication plans for this design, (b) shows the Pareto front generated by joint exploration of both the design variants and fabrication plans for the chair, where each point is a (design, fabrication plan) pair. Design variations indicate different ways to compose the same 3D model from a collection of parts and are illustrated with the same color in the Pareto front. A physical chair is fabricated by following the result fabrication plan. The Pareto front of joint exploration dominates the Pareto front of (a), which shows that the fabrication cost can be significantly improved by exploring design variations.
Abstract
Past work on optimizing fabrication plans given a carpentry design can provide Pareto-optimal plans trading off between material waste, fabrication time, precision, and other considerations. However, when developing fabrication plans, experts rarely restrict to a single design, instead considering families of design variations, sometimes adjusting designs to simplify fabrication. Jointly exploring the design and fabrication plan spaces for each design is intractable using current techniques. We present a new approach to jointly optimize design and fabrication plans for carpentered objects. To make this bi-level optimization tractable, we adapt recent work from program synthesis based on equality graphs (e-graphs), which encode sets of equivalent programs. Our insight is that subproblems within our bi-level problem share significant substructures. By representing both designs and fabrication plans in a new bag of parts (BOP) e-graph, we amortize the cost of optimizing design components shared among multiple candidates. Even using BOP e-graphs, the optimization space grows quickly in practice. Hence, we also show how a feedback-guided search strategy dubbed Iterative Contraction and Expansion on E-graphs (ICEE) can keep the size of the e-graph manageable and direct the search toward promising candidates. We illustrate the advantages of our pipeline through examples from the carpentry domain.
Video
More results
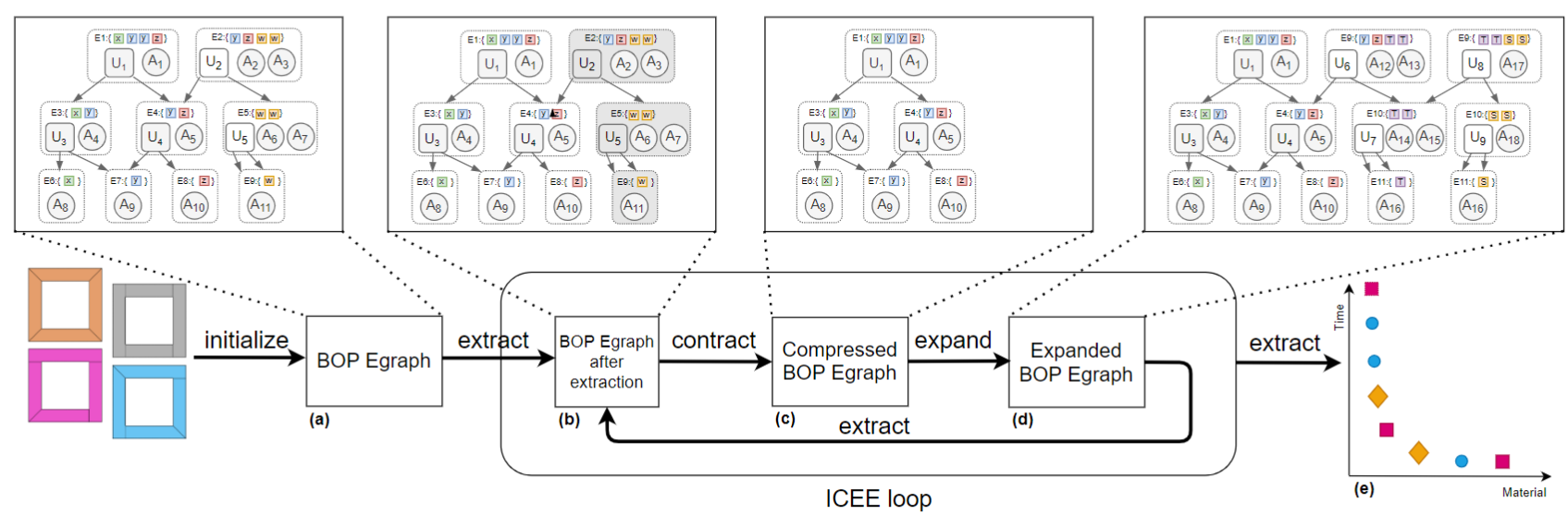
Algorithm overview: the first step initializes a BOP E-graph (Section 4.3.2, Section 4.3.3) with several design variants and a small number of fabrication arrangements (a). U and A represent union and atomic e-nodes respectively. As part of the ICEE loop, the algorithm extracts a Pareto Front (Section 4.3.4) which is used to score the e-classes in the BOP E-graph (b). For example, the gray e-class containing a “U” and an “A” e-node indicates a low score, i.e., the e-class did not contribute to Pareto-optimal solutions. The BOP E-graph is then contracted (Section 4.3.5) by removing the low-scored e-classes (and their parent e-nodes) to get a compressed BOP E-graph (c). As described in Section 4.3.6, this contracted BOP E-graph is then further expanded (d) by exploring more design variants and fabrication arrangements. The algorithm exits the loop when the termination conditions are reached, returning the final Pareto Front (e).
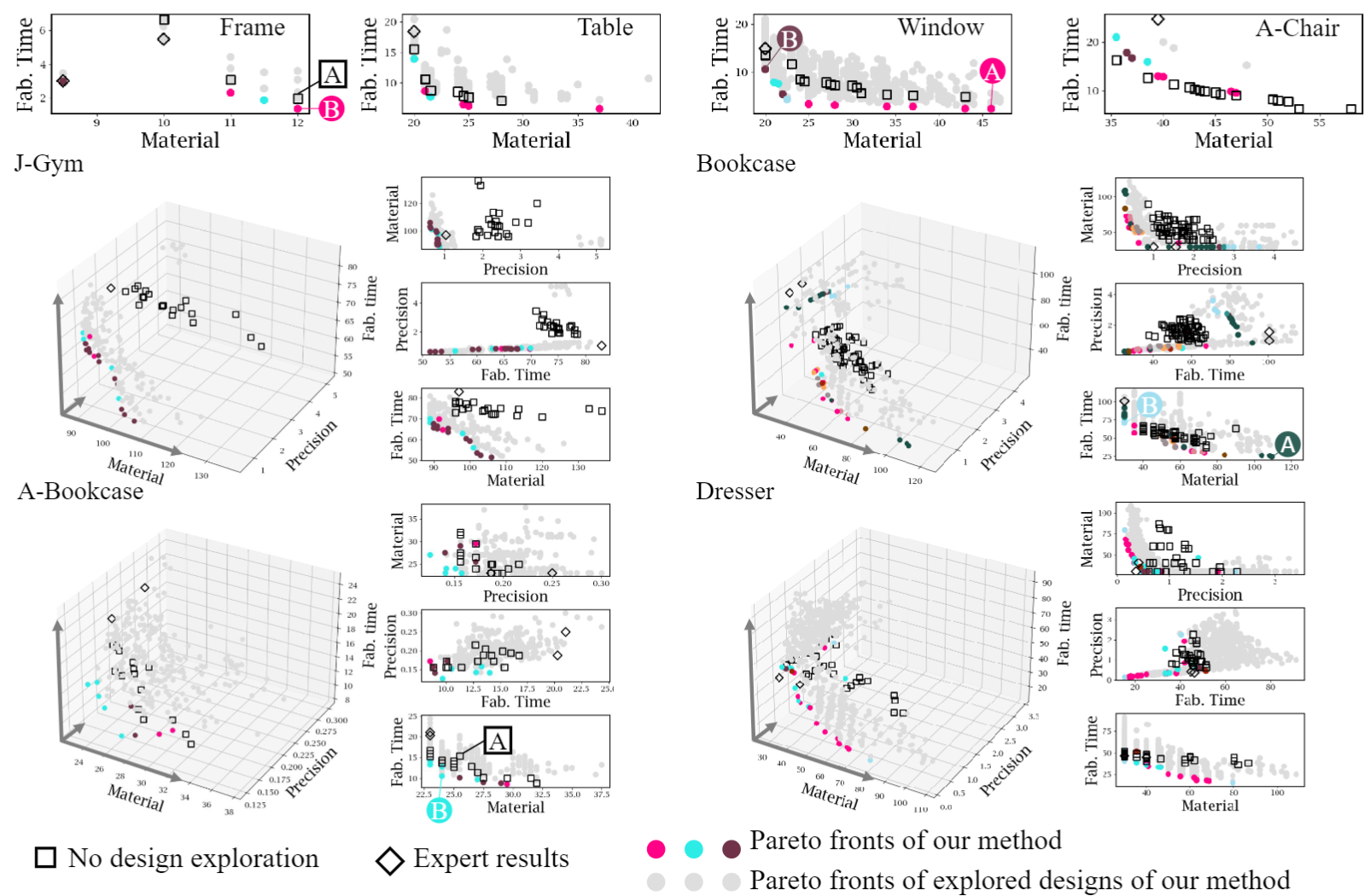
Pareto fronts computed from our pipeline with design optimization as colored dots. Each color corresponds to a different design. The gray dots indicate
the Pareto fronts of all explored design variations. These are compared against Pareto fronts computed without design optimization (fabrication optimization
only, using the original model as the input design) as squares, and expert fabrication plans as diamonds. Often, fabrication plans from a design variant are
more optimal than those generated from an input design. For the unit of objective metrics, material usage (,) is in dollars, cutting precision (𝑓𝑝 ) is in inches,
fabrication time (
,) is in minutes.

Two examples where searching the design space revealed fabrication plans that completely dominated the fabrication plans generated for the input design.
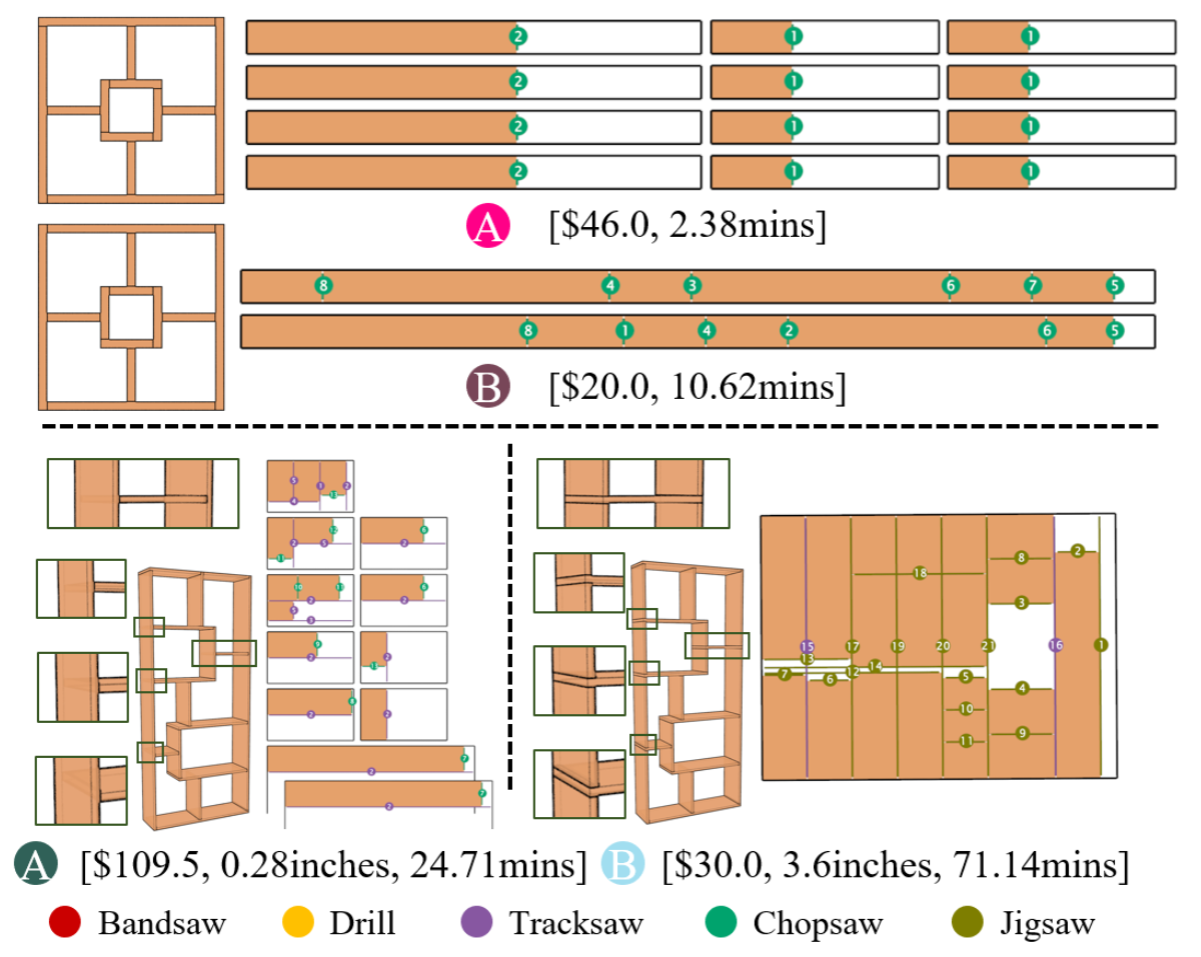
Two examples where exploring different designs lead to a wider diversity of plans, where each tradeoff on the Pareto front is only possible because of the underlying design.
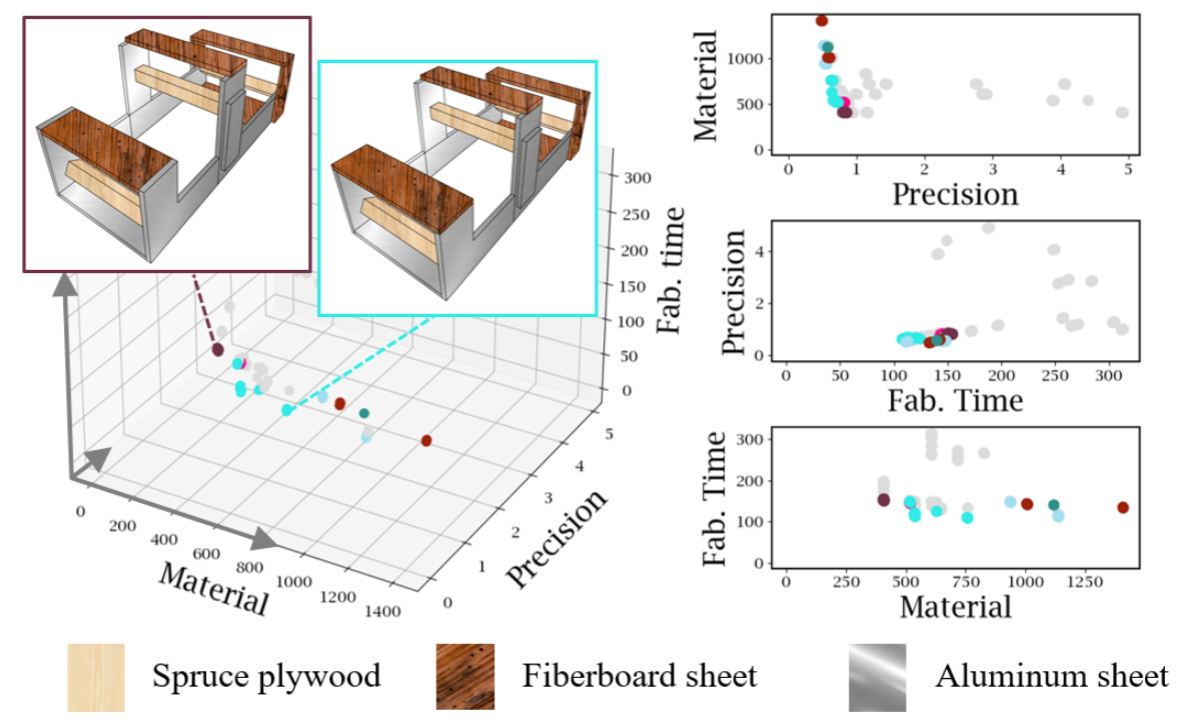
A loom model with mixed material where two kinds of wood (spruce plywood and medium density fiberboard sheet) and one kind of metal (aluminum sheet) are assigned to each part.
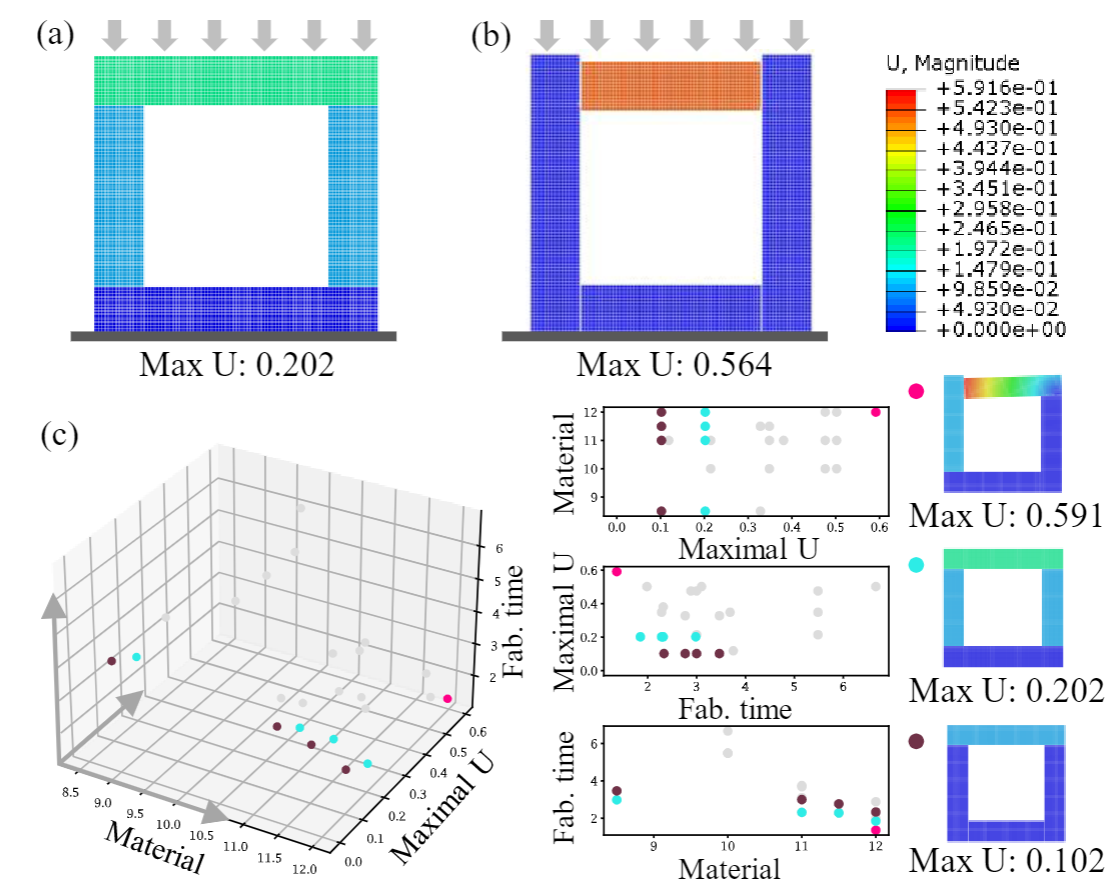
Pareto fronts computed from by our pipeline for the Frame model with three objective functions, material usage , fabrication time
, and stability performance. The physical stability of each design variation is simulated with Abaqus/CAE 2021, measured with the maximal displacement (Max U). All displacements are in inches. In this figure, (a) is the displacement visualization in a direction, (b) is the displacement visualization of the same design but with a different direction, (c) plots the Pareto fronts computed from our pipeline where three design variations are selected.
Downloads
 |
 |
 |
 |
 |
| Paper | Supplementary | Slides (coming) | Code (coming) | Bibtex |
@article {zhao2022co,
author = {Zhao, Haisen and Willsey, Max and Zhu, Amy and Nandi, Chandrakana and Tatlock, Zachary and Solomon, Justin and Schulz, Adriana},
title = {Co-Optimization of Design and Fabrication Plans for Carpentry},
journal = {ACM Transactions on Graphics (TOG),
note = {presented at SIGGRAPH 2022},
volume = {41},
number = {3},
pages = {1--13},
year = {2022}
publisher={ACM New York, NY}
}
Acknowledgement
The authors would like to thank anonymous reviewers for their helpful feedback; Haomiao Wu for her contribution to the algorithm development in the early stage of the project; Elias Baldwin, David Tsay, Alexander Lefort, and Qiyang Tan for helping the experiments.
This material is based upon work supported by the National Science Foundation under Grant Nos. CCF-2017927, IIS-1954028, IIS-1838071, 1749570 and 1813166. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. The work is also supported by the Google faculty award and the NSF China (62072284). Solomon acknowledges the generous support of Army Research Office grant W911NF2010168, of Air Force Office of Scientific Research award FA9550-19-1-031, from the CSAIL Systems that Learn program, from the MIT–IBM Watson AI Laboratory, from the Toyota–CSAIL Joint Research Center, from a gift from Adobe Systems, from an MIT.nano Immersion Lab/NCSOFT Gaming Program seed grant, and from the Skoltech–MIT Next Generation Program.