Build-to-Last: Strength to Weight 3D Printed Objects

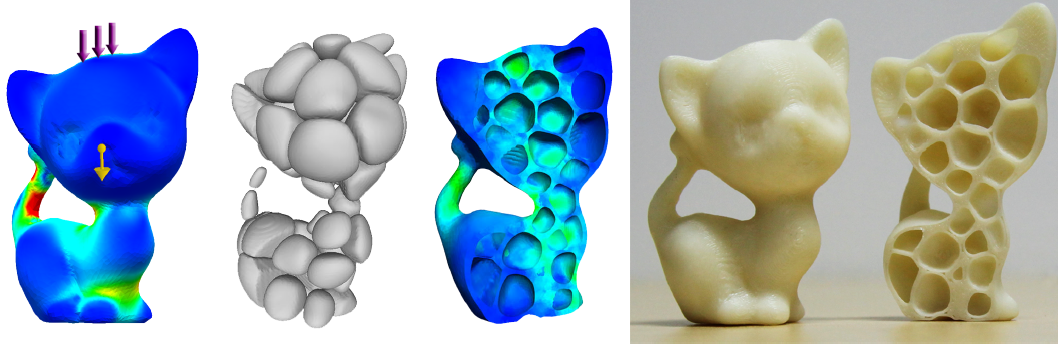Figure 1: We reduce the material of a 3D kitten (left), by carving porous in the solid (mid-left), to yield a honeycomb-like interior structure which provides an optimal strength-to-weight ratio, and relieves the overall stress illustrated on a cross-section (mid-right). The 3D printed hollowed solid is built-to-last using our interior structure (right).

Abstract: The emergence of low-cost 3D printers steers the investigation of new geometric problems that control the quality of the fabricated object. In this paper, we present a method to reduce the material cost and weight of a given object while providing a durable printed model that is resistant to impact and external forces.

We introduce a hollowing optimization algorithm based on the concept of honeycomb-cells structure. Honeycombs structures are known to be of minimal material cost while providing strength in tension. We utilize the Voronoi diagram to compute irregular honeycomb-like volume tessellations which define the inner struc ture. We formulate our problem as a strength-to-weight optimiza tion and cast it as mutually finding an optimal interior tessellation and its maximal hollowing subject to relieve the interior stress. Thus, our system allows to build-to-last 3D printed objects with large control over their strength-to-weight ratio and easily model various interior structures. We demonstrate our method on a collection of 3D objects from different categories. Furthermore, we evaluate our method by printing our hollowed models and measure their stress and weights.

Video:

 

Downloads:

• Paper [PDF, 27MB]
• Demo Video [ZIP, 29.7MB]
• Presentation Slides [PPTX, 44.3MB]
• Models [ZIP, 39.1MB]

BibTex:

  @ARTICLE{Lu:2014,
       author = {Lin Lu, Andrei Sharf, Haisen Zhao, Yuan Wei, Qingnan Fan, Xuelin Chen, Yann Savoye, Changhe Tu, Daniel Cohen-Or, Baoquan Chen},
       title = {Build-to-Last: Strength to Weight 3D Printed Objects},
       journal = {ACM Trans. Graph. (Proc. SIGGRAPH)},
       year = {2014},
       month = {August},
       volume = {33},
       number = {4},
       pages = {97:1--97:10},
      }